| Assigned: | March 1 |
| Design due: | March 9, 11:59pm |
| First version due: | March 29, 11:59pm |
| Second version due: | April 10, 11:59pm |
Read the entire assignment before you start working on it.
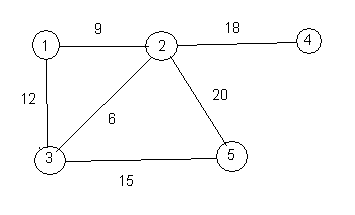
This assignment involves weighted graphs, as described in assignment 3. For example, the following is a weighted graph.

Two vertices are said to be adjacent if there is an edge that connects them directly to one another. In the graph above, vertices 1 and 2 are adjacent, but 1 and 4 are not adjacent.
Think of the vertices of a graph as towns and the edges as roads. The weight of an edge is the length of the road. One thing that you might like to know is how to get from one town to another by the shortest possible route. For example, in the weighted graph above, the shortest route from vertex 1 to vertex 5 is to go from 1 to 3 and then from 3 to 5, and the length of that route is 27. You add the weights of the edges that you use.
Write an application that reads a weighted graph from the standard input, in the same format as for programming assignment 3. For this assignment, however, the edge weights are real numbers. After the description of the graph will be two vertex numbers, s and t. For example, the input might look like this.
5 1 2 9.0 1 3 12.0 2 4 18.0 2 3 6.0 2 5 20.0 3 5 15.0 0 1 5The input says that there are five vertices. There is an edge from vertex 1 to vertex 2, with weight 9.0, etc. The start vertex s is 1, and the end vertex t is 5.
Your program should print the graph, followed by the shortest path from s to t and the distance from s to t via that path, on the standard output. The example input might lead to the following output.
There are 5 vertices. The edges are as follows. (1,3) weight 12.000 (1,2) weight 9.000 (2,5) weight 20.000 (2,3) weight 6.000 (2,4) weight 18.000 (3,5) weight 15.000 The shortest path from 1 to 5 has length 27.000 and is 1 -> 3 -> 5
Please make the last two lines of your output have the form shown above, where the last line shows the path from s to t, with -> between vertices, and the line before that has the form shown.
There is an algorithm called Dijkstra's algorithm that you can use to find shortest paths. This section describes how that algorithm works.
You will need to store some information for each vertex in the graph.
Each vertex has a status value (one of Done, Pending or Peripheral). A vertex with status Done is called a done vertex, a vertex with status Pending is called a pending vertex, and a vertex with status Peripheral is called a peripheral vertex.
Each vertex has a current distance from the start vertex. For convenience I will write dist(v) in this section for the current distance value stored for vertex v. Do not presume that this is C++ notation.. You might write g.info[v].distance in your program, or something else, depending on how you define the Graph type.). You will rarely find that an algorithm is described in exactly the terms that you will use for a particular implementation of that algorithm.
We will build up the shortest path backwards, indicating, for each vertex v, how to get from v back to the start. Each vertex has a current next-vertex, which is the next vertex to go to on the way to the start. For convenience I will write next(v) for the current next-vertex stored with vertex v. Again, this is not intended to be the way you will write this in your C++ program.
Each vertex has a linked list of edge descriptions, where each list cell holds another vertex and a weight. These are the vertices that are adjacent to this vertex, and this list is called the adjacency list of this vertex. This is described in more detail in the design section.
A done vertex v has been finished, and dist(v) is the correct shortest distance from v to the start, s. The shortest path from v to s begins by going to next(v). It continues to vertex next(next(v)), then to next(next(next(v))), etc. until it reaches s.
A pending vertex v is adjacent to at least one done vertex, but is not done. When v is pending, dist(v) is the shortest distance from v to s, provided there is a restriction that the path taken from v to s must begin by going from v to a done vertex. (There might be shorter paths that begin with an edge from v to a vertex that is not yet done.) When v is pending, the currently best known way to get from v to s is to start by going to next(v), and continuing by the shortest path to s from there.
A peripheral vertex is one that is neither done nor pending. Its current distance and next-vertex values are meaningless. There is no edge between any done vertex and any peripheral vertex.
The algorithm begins by marking the start vertex s as done and setting dist(s) to 0. Each vertex v that is adjacent to s is marked pending, with dist(v) set to the weight of the edge between v and s, and next(v) set to s. All other vertices are marked peripheral.
After initializing, the algorithm repeatedly performs phases, until vertex t (the target vertex) is done, or there are no more pending vertices. Each phase works as follows.
| One phase |
|---|
|
When the algorithm is finished, you will be able to follow a path from t back to s by following the chain of next vertices.
t -----> next(t) -------> next(next(t)) ----> ... -----> s
Print that chain out backwards, so that it goes from s
to t instead of from t to s.
The easiest way to do that is
to use recursion. To print a path backwards, starting at vertex u,
print the path starting at next(u) backwards, then print u.
Of course, in the special case where u is the start vertex
s, just print s.
Dijkstra's algorithm needs to be able to find a pending vertex that has the smallest possible distance. One way to do that is to look at every vertex. But that can be expensive when there are many vertices. An alternative is to put the pending vertices into a specialized data structure that is good for locating smallest things. Such a data structure is called a priority queue.
A priority queue holds a collection of items, each having a priority attached to it. (So the members of a priority queue are structures.) For our purposes, each item is an integer, and each priority is a real number. When a priority queue is created, it is empty. That is, it has no items in it.
The following operations are available for a priority queue q.
Insert a item v with priority p into priority queue q.
Remove the item from the queue that has the lowest priority, and set variable v to that item, and p to its priority. The parameters of remove must be reference parameters. Logically, they are out-parameters, since they represent information being sent from the remove function to its caller, not the other way around. If the queue is empty, remove should set v = 0 and p = 0.
Replace the priority of value v in the queue by p.
Return true if q is empty.
See below for suggestions on how to implement priority queues.
You can use a priority queue to keep track of the pending vertices. When a vertex is marked pending for the first time, insert it into the queue, with its current distance being its priority. When the distance of a pending vertex is updated, also update it in the queue. To find the pending vertex with the smallest distance, use the remove function to get it from the priority queue.
Create a module consisting of two files, graph.h and graph.cpp, that is responsible for graphs and Dijkstra's algorithm.
You will need a method of storing a graph. Store the graph as a structure, containing a pointer to an array that has an index for each vertex. Also store the size of the array in the structure.
With each vertex, store all of the information required by Dijkstra's algorithm, including a linked list of the vertices that are adjacent to this vertex, each with the weight of the edge. For example, the graph shown above would be represented as follows. The upper number in each list cell is a vertex number, and the lower number is the edge weight. (Remember that the weight is, in general, a real number.) The ... parts of the array are the other information (status, distance, next).

Provide functions to do the following tasks.
Read a graph, in the format described under the requirements. Build up the adjacency lists as you read the graph. An edge from u to v needs to be put into two lists, the one for u and the one for v.
Print a graph. You only want to show each edge once. Scan each adjacency list, but only print an edge when it goes to a higher numbered vertex, to avoid printing it twice. You will want a function that prints the edges in an adjacency list that go to higher numbered vertices, so that you can call that function for each vertex.
Run Dijkstra's algorithm, filling in the extra information. You will probably want helper functions to keep things easy.
Print the path from s to t that was found by Dijkstra's algorithm.
You should be able to work out contracts and prototypes for these functions.
Create a module that implements priority queues. It should have two files, pqueue.h and pqueue.cpp. Provide a type and all of the functions.
Create a separate module, main.cpp, that holds the main program. The main program should (by calling functions) read the graph, print the graph, read s and t, run Dijkstra's algorithm, and print the results from Dijkstra's algorithm.
You can use an enumerated type to create the type of status values. The following line defines constants Done, Pending and Peripheral, of type StatusType.
enum StatusType {Done, Pending, Peripheral};
There are some clever and efficient ways of implementing priority queues. However, we will not try to use any of them here. Instead, we will adopt a simple approach that is less efficient. But later on you could replace this simple implementation with a more efficient one. It is critical that your implementation of graph.cpp does not use any details of the priority queue implementation, so that pqueue.cpp and pqueue.h can be replaced later by a better implementation without making any changes to graph.cpp or graph.h.
Represent a priority queue as a linked list, storing an item and its priority in each list cell. Keep the list in ascending (or, really, nondescending) order of priority. So the item with the smallest priority is at the front of the list.
The remove function is very easy, since the item to remove is at the front of the linked list.
You will find the insert function very easy to implement if you use recursion. The new item either belongs at the beginning of the list or it doesn't. If it belongs at the beginning of the list, just create a new list cell and install it at the beginning. If the new item does not belong at the beginning, a recursive call to insert will finish the job.
You will want an auxiliary function to remove a given item from the list. This function is not to be used by any other module, since it is not an official part of the priority queue implementation. (A more efficient implementation of priority queues might not be able to handle removal of an arbitrary member.) Again, recursion makes this very easy.
To do an update, just remove the item and re-insert it with a new priority. Do not try to be excessively efficient. Remember that, if you find that you need efficiency in this module, you will want to throw away this entire way of implementing it, and use a more efficient data structure, so don't waste your time trying to make this one really efficient.
Here is a suggested plan for implementing this program.
Create all of the files. Define the types in the appriate files. Add contracts and prototypes for the functions. Make sure that each contract is clear and concise, and tells what the function does, not how it works. Check that the purpose of each parameter is clear.
Implement the insert and remove functions in the priority queue module. Add a function that prints the contents of the list. Instrument your insert and remove functions. That can be awkward for a recursive function. The way to do that is to use a wrapper function that does the instrumentation, and that uses another function to do the work. Here is a wrapper function for insert. It presumes that the real insert function (that performs the insertion) is called doInsert, and that it takes, as a parameter, a linked list pointer called q.ptr.
void insert(PQueue& q, int v, double p)
{
# ifdef DEBUG
cout << "Inserting item " << v << " with priority " << p << "\n";
cout << "Current queue: ";
printQueueList(q.ptr);
cout << "\n";
# endif
doInsert(q.ptr, v, p);
# ifdef DEBUG
cout << "Done inserting: ";
printQueueList(q.ptr);
cout << "\n";
# endif
}
Implement the remaining priority queue functions. Test them.
Implement the function that reads a graph, and the function that prints a graph. Test them, by reading and printing a graph.
Implement Dijsktra's algorithm. Test it. Just print the information in the array in a raw form to see that it is right. Your main function should be growing in the direction of the final version.
Implement the function that prints the path. Test it. Your main program should have reached the final version now.
After you are confident that your program works, submit it.
To turn in this program, log into one of the Unix computers in the lab. (You can log in remotely.) Ensure that your files are there. Change to the directory that contains those files. Then issue one of the following commands.
submit 4a graph.cpp graph.h pqueue.cpp pqueue.h main.cpp
submit 4c graph.cpp graph.h pqueue.cpp pqueue.h main.cpp
submit 4c graph.cpp graph.h pqueue.cpp pqueue.h main.cpp