
| Assigned: | February 14 |
| Design due: | February 20, 11:59pm |
| First version due: | March 1, 11:59pm |
| Second version due: | March 21, 11:59pm |
Read the entire assignment before starting on it.
A graph is a collection of vertices connected by a collection of edges. An edge connects exactly two vertices to one another. You can draw a picture of a graph by showing the vertices and the edges connecting them. Here is an example. The vertices are shown as circles with numbers in them and the edges are lines connecting the vertices.

We will only be concerned with connected graphs. A graph is connected if there is a path from every vertex to every other vertex, following edges. For example, in the above graph, there is a path from 3 to 4 that goes (3, 1, 2, 4). There are other paths from 3 to 4 as well.
A weighted graph is a graph in which each edge has a number attached to it, called the weight of the edge. Here is a picture of a weighted graph.
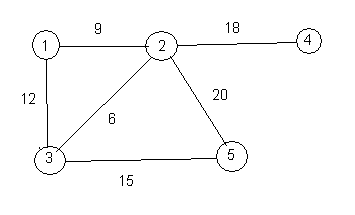
A spanning tree of a graph is obtained by deleting as many edges as possible, without making the graph so that it is no longer connected. That is, we still need to have a path from each vertex to each other vertex. For example, the following is a spanning tree of the above weighted graph.
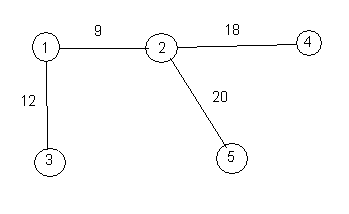
The weight of a spanning tree is the sum of the weights of its edges. For example, the weight of the above spanning tree is 59. Here is another spanning tree for the same graph. Its weight is 48.
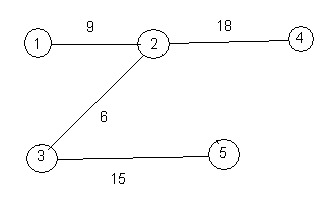
Obviously, some spanning trees have smaller weight than others. A minimal spanning tree is a spanning tree with the smallest possible weight.
Write a program that reads a description of a weighted graph, and prints the edges that are part of a minimal spanning tree of that graph, and also prints the total weight of the minimal spanning tree. The input should be read from the standard input (cin), and the output should be written to the standard output (cout).
The input starts with a line that tells how many vertices the graph has. If there are five vertices, then those vertices have numbers 1, 2, 3, 4 and 5. In general, if there are n vertices, then they are numbered 1, ..., n.
Following the first line are the edges, one per line. Each edge line has three integers on it. Line
2 4 50indicates that there is an edge between vertices 2 and 4, and that its weight is 50. The end of the input is signaled by a line that contains just a 0. An input describing graph

might look like this.
5 1 2 9 1 3 12 2 4 18 2 3 6 2 5 20 3 5 15 0
You can assume that there are no more than 100 edges, but that number must be easy to change. To increase this to 200, for example, should only require changing one line of your program.
The output of your program for this input might look like this.
The input graph has 5 vertices, and its edges are as follows. vertices weight 1 2 9 1 3 12 2 4 18 2 3 6 2 5 20 3 5 15 A minimal spanning tree uses the following edges. vertices weight 2 3 6 1 2 9 3 5 15 2 4 18 The total weight of the spanning tree is 48.
Your program is not required to insist that the three numbers that describe an edge are on one line, but it can if it wants to. For example, if your program allows an input like the following, that is acceptable. But your program is not required to allow such inputs. (You will find it easier to allow these additional input forms.)
5 1 2 9 1 3 12 2 4 18 2 3 6 2 5 20 3 5 15 0The only difference between this and the previous input is the placement of line breaks.
Important note. The first number in the input is the number of vertices, not the number of edges. The only way you can determine the number of edges is by reading them and counting them.
Important note. The last line has only one number on it, not three.
For this problem, the algorithm is sufficiently difficult that it is a good idea to think about the algorithm before proceeding with the design.
There is a well-known algorithm, called Kruskal's algorithm, for computing a minimal spanning tree of a weighted graph. It goes as follows.
Sort the edges from small weight to larger weight. Call the sorted list of edges e1, ..., em. So, for example, e1 is the edge with the smallest weight.
Start with an empty graph K. It has all of the vertices, but no edges yet. Edges will be added to it until, at the end, it is the minimal spanning tree.
For i = 1, ..., m do
See below for an argument that Kruskals algorithm works.
A tricky issue with Kruskal's algorithm is how to determine whether two vertices are already connected by a path. Suppose we write u ~ v is there is a path between u and v. You have probably seen the notion of an equivalence relation (in CSCI 2427). Notice that ~ is an equivalence relation. That is,
(~ is reflexive) u ~ u. That is, you can always get from u to itself (by taking no edges).
(~ is symmetric) If u ~ v then v ~ u. That is, if there is a path from u to v, then there is also a path from v to u.
(~ is transitive) If u ~ v and v ~ w then u ~ w. If there is a path from u to v and also a path from v to w, then there is a path from u to w.
An equivalence relation is always characterized by its equivalence classes. That is, at any point in time, you can characterize which vertices are connected to which others by writing a collection of sets of connected vertices. For example, suppose that there are 6 vertices. Sets
{1,3,4}, {2,5}, {6}indicate that vertices 1, 3 and 4 are connected to one another, vertices 2 and 5 are connected to one another, and vertex 6 is not connected to any other vertex. Only vertices that are in the same set are connected to one another.
Look at what Kruskal's algorithm needs to do with this collection of sets.
It needs to be able to ask whether two vertices are in the same set. That is, are they already connected by a path?
It can add an edge, which causes two of the sets to be combined. For example, if it starts with
{1,3,4}, {2,5}, {6}and adds an edge from 3 to 5, then sets {1,3,4} and {2,5} get combined, yielding a new collection of sets
{1,2,3,4,5}, {6}
If we can figure out a way to handle a collection of sets, with an operation to test whether two numbers are in the same set, and another operation that combines two of the sets in to one, then we will be able to implement Kruskal's algorithm.
An algorithm for of this part of the program is discussed below.
Now, with the basics of the algorithms outlined, we can design the program. This program should have three modules.
Module 1 implements the equivalence handling. It should consist of two files, equiv.h and equiv.cpp. In equiv.h, define a structure type Equiv, holding just one variable, a pointer to an array of integers. See the description of the equivalence manager algorithm for the intent of the array. Write contracts and prototypes for two functions, together(e,x,y) and combine(e,x,y). The idea is that together(e,x,y) returns true if x and y are in the same set, as described by equivalence relation e, and combine(e,x,y) modifies e so that the sets containing x and y are combined in to a single set. The headings are as follows.
bool together(Equiv& e, int x, int y); void combine(Equiv& e, int x, int y);File equiv.cpp contains implementations of functions, including helper functions. Every function must have a contract.
Module 2 implements Kruskal's algorithm. Keep it simple. In file graph.h, create a structure type Graph, where a graph stores
You will also want a structure type that represents one edge. Create the following functions, and add prototypes and contracts for them to graph.h. Put the implementations of these functions into graph.cpp.
A function that reads information about a graph, in the format shown in the requirements section, and that returns a graph holding the information that it read.
A function to print a graph, by telling how many vertices it has, how many edges it has, and then showing the edges. It should not print any specific heading. For example, it should not say that it is printing the input graph. Just provide information about the graph.
A function to compute the total weight of a graph, by adding up the weights of the edges.
A function that takes a graph G as a parameter, and returns another graph that is a minimal spanning tree of G. This function contains an implementation of Kruskal's algorithm.
Module 3 contains only a main program. Call it main.cpp. It should include graph.h, but not equiv.h. The main program should be short. It just does the following steps.
Do not confuse edges with vertices. Keep track of the number of vertices in a graph separately from the number of edges.
The vertices are numbered 1, ..., n. You will need to have an array of edges. It is a good idea to start numbering the edges from 0, not from 1. So put the first edge that you read at index 0 in the array.
You will need to sort the array of edges according to the weights of the edges. There is a function in the library, called qsort, that will sort an array. It implements a variant of the Quicksort algorithm. You should include header file <cstdlib> to use qsort.
Qsort is a general sorting function, designed to be able to sort any type of array into any desired order. In order to achieve this degree of generality, qsort needs information about the array and how to sort it. It also needs for you to perform some conversions that, in general, would be questionable, but that work correctly here.
Qsort takes four parameters. In general, you write
qsort(base, numEl, elSize, compar);where
Parameter base is a pointer to the array that you want to sort. You should convert this pointer to type (void*).
Parameter numEl is the number of elements in the array.
Parameter elSize is the number of bytes occupied by each element. If each thing in the array has type Edge, then this should be sizeof(Edge).
Parameter compar is a function. (C++ allows you to pass a function as a parameter to another function. You do not run the function yourself; qsort will run it for you.) Function compar takes two parameters, which will be pointers to particular members of the array when qsort calls it. compar(A, B) should return
if A should come before B in the sorted array
if A should come after B in the sorted array
if you do not care what order they are in
Your comparison function might look like this.
int compareEdges(const Edges* A, const Edge* B)
{
return A->weight - B->weight;
}
To run qsort, define a new type, QSORT_COMPARE_TYPE, as follows. It is the type of the compar parameter that qsort expects to receive.
typedef int (*QSORT_COMPARE_TYPE)(const void*, const void*);Now statement
qsort((void*) Arr, n, sizeof(Edge), (QSORT_COMPARE_TYPE)compareEdges);will sort array of edges Arr.
Your function, compareEdges, does not have type QSORT_COMPARE_TYPE, since compareEdges takes two parameters of type Edge*, and qsort says that it should take two parameters of type void*. But you can tell the compiler to ignore this, and to let you pass your compareEdges function to qsort, by doing a cast, which tells the compiler to treat a value of one type as if it is a value of a different type. In most cases, this is a very dangerous thing to do, but you have to do it to use qsort.
Programs often need to use tools that are provided as abstract data types. An abstract data type is a type of data, along with some operations. An object that belongs to the data type remembers some information, and the operations either get or modify that information.
You need an abstract data type that manages equivalence classes of positive integers. This section describes the abstract data type in a little more detail, and tells you a simple way to implement it.
The conceptual view is how somebody who uses the abstract data type thinks about it. You create an Equiv object by telling it a positive integer n. You write
Equiv e(n);to create an object e that manages an equivalence relation (a collection of disjoint sets) over 1, ..., n.
Two functions are available.
This returns true if x and y are currently in the same set in object e, and false if they are in different sets.
This makes x and y equivalent, combining the sets that contain them.
The following shows an example. The result of a combine operation is the new collection of sets. The result of a together operation is either true or false. The example is for the case where n = 7.
| Operation | Result |
|---|---|
| {1} {2} {3} {4} {5} {6} {7} | |
| combine(e,3,6) | {1} {2} {3,6} {4} {5} {7} |
| combine(e,4,5) | {1} {2} {3,6} {4,5} {7} |
| together(e,3,6) | true |
| together(e,4,6) | false |
| combine(e,3,5) | {1} {2} {3,4,5,6} {7} |
| combine(e,3,1) | {2} {1,3,4,5,6} {7} |
| together(e,3,4) | true |
| together(e,1,6) | true |
| together(e,2,4) | false |
| combine(e,3,5) | {2} {1,3,4,5,6} {7} |
Notice that you are allowed to combine two numbers that are already in the same set. Nothing happens then.
There is a simple way to implement the Equiv abstract data type. The idea is to have a leader of each set. For example, if numbers 3, 5 and 8 are in the same set, then they might decide that 5 is their leader. You write a function leader(k) that returns the leader of the set that contains k. Then, to find out whether two numbers are in the same set, just check whether they have the same leader.
To implement the leader function, use another idea that is related to leaders. Each number that is not a leader has a boss. The boss of a number might be that number's leader, or it might not. But the boss is closer to the leader. You find your leader by going to your boss, then to your boss's boss, etc, until you hit a number that does not have a boss. To indicate that a leader does not have a boss, we will say that its boss is 0. So, if e.boss[k] is k's boss (in object e), then you can find e's leader as using the following loop.
r = k; while(e.boss[r] != 0) r = e.boss[r];Now r is k's leader.
When you combine two sets, you start by getting the leaders of those sets. Be careful; if the leaders are the same, do not make any changes. But if the leaders are different, then make one of those leaders be the boss of the other. For example, if x and y are two leaders, then
e.boss[x] = y;makes y be x's new boss. It is critical that you only change the boss of a leader.
Here is a suggestion for how to write this program.
Write type definitions. Write contracts and heading for all of the functions. Put them where they go. For example, the definition of the Equiv type goes in equiv.h. The definition of the Graph type goes in graph.h. The contract and heading for the leader function go in equiv.cpp, not in equiv.h. Nobody is supposed to use the leader function except equiv.cpp. Submit your design.
Implement the functions in equiv.cpp. Add one more function that prints the boss array, for testing. Instrument the combine function so that it can show the boss array before and after it runs. Write a separate main program that tests your implementation of this module. Print the result of each together call. Be sure to try cases where you are combining things that are already together. Test thoroughly. Do not throw away your tester.
Implement the functions that read and print a graph. Write part of the main function in main.cpp. Just have it read the graph and print it. Test this.
Implement the function that computes the total weight of a graph. Add a line to your main program that computes the total weight of the input graph. Test it.
Implement the function that computes the minimal spanning tree. Modify your main program to use this, and to do the entire job, according to the requirements. Test it on several different graphs. Do not try just one graph. Now that you have a working version, save it. If you make more modifications, modify a copy.
If you have time, implement the extra credit parts. Test them carefully. Do not make the mistake of just writing something and then doing shoddy testing. Actually look at the results of your tests. Notice that you are modifying equiv.cpp. Instead of just running your application, try running your tester that was designed for testing equiv.cpp. You will get better testing that way.
Submit your work.
To turn in this program, log into one of the Unix computers in the lab. (You can log in remotely.) Ensure that your files are there. Change to the directory that contains those files. Then issue one of the following commands.
submit 3a equiv.cpp equiv.h graph.cpp graph.h main.cpp
submit 3b equiv.cpp equiv.h graph.cpp graph.h main.cpp
submit 3c equiv.cpp equiv.h graph.cpp graph.h main.cpp
For extra credit, implement two improvements on the algorithm for managing equivalence classes. But do so carefully.
You will only receive extra credit for an improvement that is implemented correctly.
If your "improvement" actually breaks the implementation, so that it gives incorrect results, you will receive less credit for the "improved" version than you would for a correct version without any improvements.
For simplicity, instead of e.boss, I will just write boss in this section.
The first improvement involves a change to the leader function. After the leader function scans through a chain of boss links to find the leader of a number, it should go back through the chain and put the genuine leader in the boss array for every number that was looked at in the chain. That way, subsequent leader computations will go much more quickly. For example, if the boss array contains
boss[1] = 2 boss[2] = 4 boss[3] = 0 boss[4] = 6 boss[5] = 3 boss[6] = 0 boss[7] = 4 boss[8] = 5then computing leader(1) requires chaining through 1, 2, 4, 6, stopping at leader 6. The improvement adds another loop that changes the contents of the boss array to the following, by installing the correct leader (6) of each of the numbers that was looked at.
boss[1] = 6 boss[2] = 6 boss[3] = 0 boss[4] = 6 boss[5] = 3 boss[6] = 0 boss[7] = 4 boss[8] = 5It is just a matter of rescanning through the chain, the same way the chain was scanned the first time, but now putting the leader into the array as you go.
Notice that we have not scanned the entire boss array from beginning to end! Boss[8] is still 5, even though the leader of 8 is 3. Only the numbers that were looked at in the original scan have their boss values changed. If you try to change everything in the array, you make the implementation slower, not faster.
Also notice that it was not just the boss of 1 that was changed. All of the numbers that were examined in the chain have their bosss set to their leaders. For example boss[2] was changed too.
Remark. If you understand recursion, you can write the leader algorithm, with the improvement, quite easily using recursion.
Each number that is a leader has a collection of constituents who have that number as their leader. For example, in the above array, number 3 is a leader, and the constituents of 3 are 3, 5 and 8. So number 3 has three constituents, counting itself. The constituent count of a leader tells how many numbers are in the set that contains that leader.
When doing a combine operation, you find two values s and t that are leaders. You can then either change the boss of s to t (so s is no longer a leader) or change the boss of t to s (so t is no longer a leader). Either one will accomplish the goal of combining the two sets, but the choice of which to do influences the efficiency of the implementation. The best choice is to change the boss of the number that has the fewest constituents. That tends to keep the lengths of the boss chains up to the leader short.
Modify the data structure so that each number has not only a boss, but also a count of its constituents. A number that is not a leader has no constituents. So now the information is an array of structures, where each structure contains a boss and a constituent count.
A picture of the initial array, before any combines have been done, might look like this. Notice that each number has one constituent, itself.
index boss numConstituents
1 0 1
2 0 1
3 0 1
4 0 1
5 0 1
6 0 1
7 0 1
When doing a combine, compare the constituent counts of the two leaders. Change the boss of the leader with the fewer constituents. (If they have the same number of constituents, then the choice is arbitrary.) If you change things so that the boss of s becomes t, then remember that all of the constituents of s become new constituents of t.
If you do combine(e,3,5) in the above array, you might arbitrarily decide to make the boss of 3 be 5. Then the array looks like this.
index boss numConstituents
1 0 1
2 0 1
3 5 0
4 0 1
5 0 2
6 0 1
7 0 1
If you now do combine(e,5,1), you must change the boss of 1,
since it has fewer constituents than 5. The array ends up looking like
this.
index boss numConstituents
1 5 0
2 0 1
3 5 0
4 0 1
5 0 3
6 0 1
7 0 1
As before, only change the boss of a number that
is currently a leader. If you now do combine(e,2,1), you
must realize that you are really being asked to combine 2 and 5, since
5 is the leader of 1. Since 5 has more constituents, you change
2, yielding
index boss numConstituents
1 5 0
2 5 0
3 5 0
4 0 1
5 0 4
6 0 1
7 0 1
As you can see, this improvement tends to lead to shorter chains
of bosses before the leader is found.
Suppose you continue by combining 6 and 7. You might get the following.
index boss numConstituents
1 5 0
2 5 0
3 5 0
4 0 1
5 0 4
6 7 0
7 0 2
Now combine 1 and 6. Their leaders are 5 and 7. Since 5 has more
constituents, change the leader of 7 to be 5. The new information
is as follows.
index boss numConstituents
1 5 0
2 5 0
3 5 0
4 0 1
5 0 6
6 7 0
7 5 0
Notice that 5 now has six constituents. Also notice that, although
6 is one of 5's constituents, its boss is 7.
The boss chains are shorter, but you still need to do the
leader calculation using a loop (or recursion).
Algorithm design requires creativity, and often requires simply feeling around until you hit on something that looks like it might work. But be careful not to stop after you have something that feels reasonable. A lot of algorithms that initially look like they will work are incorrect. You don't want to jump into writing a program that implements the algorithm when the algorithm is wrong. That is a waste of time. It is important to offer some careful reasoning about why the algorithm works before you try to implement it.
Kruskal's algorithm adds the edges starting with the cheapest ones, and, since it is supposed to find a cheapest possible spanning tree, it seems to be doing something right. But that is not justification that the algorithm works. It is only justification for investigating it to see whether it works.
This section offers an argument that Kruskal's algorithm is correct. It should be clear that Kruskal's algorithm finds a spanning tree, since it only skips over edges between vertices that are already connected by a path. The issue is whether that spanning tree is minimal. The argument is necessarily of a mathematical nature, as are most such arguments. It will probably take more than one reading for a person who is inexperienced with this kind of argument to make sense of it. But it is worth getting used to the idea of checking your algorithms carefully.
We will simplify the argument by assuming that no two edges of a graph can have the same weight. This assumption is fairly easy to get rid of, and the argument is essentially the same, but the assumption reduces the complexity of the argument.
Before trying to show that an algorithm works, you typically try looking for some counterexamples. Try to find an input that the algorithm gets wrong. Suppose that you try that for a while with Kruskal's algorithm, and are not able to find any counterexamples. Then imagine somebody else searching for counterexamples. What if that other person finds one? Think about that (unknown) counterexample, and try to convince yourself that it cannot really be a counterexample; that is, no counterexample exists.
CLAIM. Kruskal's algorithm finds a minimal spanning tree of a graph.
The argument is a kind of thought experiment. Suppose that somebody else claims to have found a counterexample demonstrating that Kruskal's algorithm does not work. We ask that person to give us the weighted graph G that the algorithm gets wrong, and the actual minimal spanning tree T for that graph. If T is not the actual minimal spanning tree, then this person is lying, and this is not considered a counterexample. Obviously, if Kruskal's algorithm fails to work, then somebody should be able to come up with both G and T, where T is the correct minimal spanning tree, and where Kruskal's algorithm gets the wrong answer.
Compute the spanning tree K produced by Kruskal's algorithm. It must be different from T or this is certainly not a counterexample.
If G has n vertices, then every spanning tree of G has exactly n-1 edges. (Try arguing that.) Since K and T do not have exactly the same edges, there must be some edge that is in T but not in K.
Look at the edges of G in the same order e1, e2, ..., em that they are looked at by Kruskal's algorithm (in ascending order of weight), and select the first one ei that is in T but not in K. Suppose that edge ei connects vertices u and v. Why wasn't ei added to tree K? Because vertices u and v were already connected by a path through edges that Kruskal's algorithm had looked at earlier. Look at that path, and look at how the same vertices are connected in T.
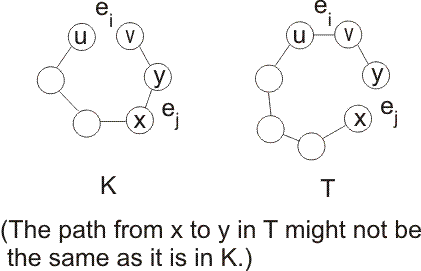
At least one of the edges ej in this path between u and v must not be in tree T. (Otherwise, T would have a cycle, and a tree cannot have any cycles.) Also, j < i, since the edges shown for K were added before edge ei was considered. Since the edges are looked at in ascending order of weight, ej must have a smaller weight than edge ei.
Make a modified tree T' by removing edge ei from T and adding edge ej. All of the vertices are still connected. (You can still get from any vertex shown in the picture to any other, so you have not cut anything off from anything else.) So T' is another spanning tree. But T' has smaller total weight than T, since we replaced a heavier edge by a lighter one. Obviously, T is not a minimal spanning tree, because T' is a spanning tree with smaller total weight.
That completes the argument. No matter what purported counterexample somebody gives us, we have shown that it cannot be a genuine counterexample. So no counterexample exists, and Kruskal's algorithm is correct for every graph.
Suppose that we have a collection of towns, and we must build railroad tracks so that it is possible for a train to get from any town to any other town. Our budget for building tracks is small, so we choose to build as little track as possible. One approach to deciding which tracks to build is to construct a weighted graph, where the vertices are the towns, and the weight of the edge from town A to town B is the length of the railroad track that would need to be built to connect towns A and B directly. Then a minimal spanning tree of that graph would be a good choice for connecting the towns, since it is the cheapest way to connect all of the towns using railroad tracks between towns.
A similar problem occurs when a house is being wired for electricity. All of the outlets on a given circuit need to be connected to the circuit panel, and to each other. To connect them with a minimum amount of wire, you might build a graph having a vertex for each outlet and for the circuit panel, with the weight between two vertices being the wiring distance between those vertices. Then get a minimal spanning tree for the graph.
(A minimal spanning tree is not always the best solution to either of these problems. You can often do better by introducing new railroad track junctions or wiring junctions, called Steiner points. For example, if you have three towns in a triangle, you can connect them together by sending tracks to a point in the middle of the triangle. The middle point is a Steiner point. But good placements of Steiner points are difficult to find, so a minimal spanning tree is a reasonable compromise.)