Computer Science 3650
Summer 2004
Solutions to Practice Questions for Exam 2

This is a closed book exam, but you may use one page of prepared notes. Answer all of the questions.

  1. Describe the main ideas behind greedy algorithms.

    Greedy algorithms are based on the idea of optimizing locally. When a greedy algorithm needs to make a choice, it chooses what will be best in the short term, without thinking about future consequences, and commits to its decision.

  2. What problem does Dijkstra's algorithm solve?

    Single source shortest paths.

  3. What problem does Prim's algorithm solve?

    Prim's algorithm computes minimal spanning trees.

  4. A vertex cover of an undirected graph G is a set S of vertices such every edge in G has at least one of its endpoints in S. The vertex cover problem is: Given an undirected graph G, find a vertex cover of G that has the smallest possible size. That is, find a set of as few vertices as possible such that every edge hits at least one of the vertices in this set. The following is a proposed algorithm for the vertex cover problem. It uses the notion of the degree of a vertex, which is the number of edges that hit this vertex.

    1. S = empty set.
    2. While G has at least one edge
    3.    Find a vertex v of the highest possible degree in G
    4.    Add v to S.
    5.    Remove vertex v from G, along with all edges that hit v
    6. Answer S.

    A vertex cover needs to cover all of the edges, where an edge is covered by choosing a vertex from that edge. This algorithm is based on the principle that, by choosing a vertex with the most edges hitting it, we get cover the most edges.

    What kind of algorithm is this? Is it guaranteed to find the smallest vertex cover? If so, why? If not, give a counterexample.

    This is a greedy algorithm, since it tries to get the most edges as possible with the next vertex, without thinking ahead.

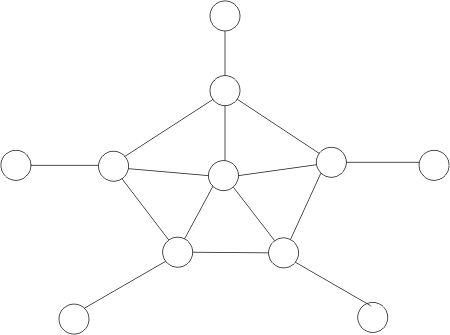
    This algorithm does not work. The following graph is a counterexample. The greedy algorithm will start by selecting the center vertex, which is the only vertex of degree 5. But the smallest vertex cover contains the five vertices that form a pentagon, and does not use the center vertex.

  5. What are the main principles of dynamic programming algorithms? That is, what characteristics do they share?

    Dynamic programming algorithms generally employ principles including

    1. Optimal substructure: optimal solutions to problems are built from optimal solutions to subproblems.
    2. "Shop around": to determine the best option, try them all and select the best one. Do not employ heuristics.
    3. Memoization: answers to subproblems are remembered to avoid repeated computation of the same thing.

  6. Dynamic programming algorithms are usually based on recursive equations. Why don't dynamic programming algorithms simply use recursion to implement those equations directly?

    Computing the equations directly using recursion results in the same thing being computed many times, and causes the algorithm to be slow. Typically, the cost of the obvious recursive algorithm is the same as the cost of the algorithm that tries all solutions.

  7. Consider the definition 

        h(0) = 1
    h(n) = h(n-1) + h(floor(n/2)) + 1
    For example, h(2) = h(1) + h(1) + 1 = 3, h(3) = h(2) + h(1) + 1 = 5, etc. An obvious algorithm to compute h is a recursive one, based directly on the defining equations. Is that algorithm efficient? Why or why not? If not, how can the algorithm be improved? Justify your answer.

    This is not an efficient algorithm because it recomputes expressions. For example, computing h(4) requires computing h(3) and h(2). But computing h(3) requires computing h(2) again. The algorithm can be improved by storing the values h(i) in an array. For i = 1,...,n, compute h[i] according to the equation, looking in the array to find h(i-1) and h(floor(i/2)). Finally, get the value h[n] from the array.

  8. There are several variants of a problem called the Knapsack Problem. One variant is as follows. The input is a list of positive integers x1, ..., xn, and another positive integer K. You would like to select some of the numbers x1, ..., xn so that their sum is as large as possible, without exceeding K. For example, if the list is 3,10,4,6,8, and K = 19, you can select 3, 10 and 6, for a sum of exactly 19. Think of these as the weights of items that you want to put into a knapsack, where the knapsack can only hold a total weight of K. You want to put as much into the knapsack as possible without overfilling it.

    A convenient way of indicating which numbers to choose it to give an index set I, telling the indices of the values in the list to take. For example, if you want to take the first, third and fourth numbers, the index set is {1,3,4}. If I is an index set, define S(I) to be the sum of all xi for i in I. For example, if I is {1,3,4}, then S(I) is x1 + x3 + x4. The Knapsack Problem is to find an index set I that is a subset of {1, ..., n} such that S(I) is as large as possible, subject to the constraint that S(I) is no larger than K.

    For w = 0, ..., K and j = 0, ..., n, let Wj, w be 1 if there is an index set I that is a subset of {1, ..., j} such that S(I) = w, and let Wj, w be 0 otherwise. In the case where j = 0, I is required to be empty. Put another way, Wj, w tells you whether it is possible to get a sum of exactly w if you are only allowed to choose from among the first j numbers in the list x1, ..., xn.

    1. Write recursive equations that define Wj, w for j = 0, ..., n and w = 0, ..., K. You can use operators and and or, which take the logical and an logical or of values, treating 0 as false and 1 as true. Your algorithm will need to use the values x1, ..., xn.

      • Wj, 0 = 1 for j >= 0 (since you can achieve a total sum of 0 by taking nothing).
      • W0, w = 0 for w > 0.
      • Wj, w = Wj-1, w or Wj-1, w-xj. (If you want to get a total sum of w using only the first j numbers, you can either use xj or not. If you choose not to use xj, then you must achieve sum w using only the first j-1 numbers. If you use xj, then you must get a sum of w - xj with the first j-1 numbers. Adding xj gives you the sum w.)

    2. The Weak Knapsack Problem does not ask for the subset I itself, but just for S(I), the largest amount that can be put into the knapsack without overfilling it. Describe an algorithm that solves the Weak Knapsack Problem in time O(nK). Assume that arithmetic and logical operations take constant time. 

         Create a two dimensional array W.
   For j = 0,...,n do W[j,0] = 1;
   For w = 1,...,K do W[0,w] = 0;
   For j = 1,...,n do
     For w = 1,...,K do
       W[j,w] = W[j-1,w] or W[j-1,w-x[j]];
   For w = K, ..., 0 do
     If W[n,w] == 1 then
       Return w.
      The idea is to use the equations from part (a), but to store them in an array to avoid repeated computation. The answer is the largest w such that Wn,w = 1.