A word to the wiseBegin working on this program right away. Do not wait. Create a refinement plan based on the plan presented below, and follow that plan. Do not attempt to write the entire program and then start testing it. Get something done for the first pass. Make your first version the best that you can. |
Read about this part, but before working on it, read the requirements at the end of the assignment.
Programs often need to use tools that are provided as abstract data types. This part has you implement an abstract data type that you will use in the next part.
This abstract data type manages sets of integers, with some somewhat unusual operations on them. Given a positive integer n, you start with a collection of sets {1}, {2}, ..., {n}, where each integer from 1 to n is in a separate set. The functions that this abstract data type supports are as follows.
Merge the sets that contain m and n into a single set.
This returns true (1) if m and n are in the same set, and false (0) if they are in different sets.
The following shows an example. The collection of sets is shown after each merge operation is performed. In the case of a together operation, the result (0 or 1) is shown.
| Operation | Result |
|---|---|
| {1} {2} {3} {4} {5} {6} {7} | |
| merge(3,6) | {1} {2} {3,6} {4} {5} {7} |
| merge(4,5) | {1} {2} {3,6} {4,5} {7} |
| together(3,6) | 1 |
| together(4,6) | 0 |
| merge(3,5) | {1} {2} {3,4,5,6} {7} |
| merge(3,1) | {2} {1,3,4,5,6} {7} |
| together(3,4) | 1 |
| together(1,6) | 1 |
| together(2,4) | 0 |
We will call this abstract data type the Merge type.
There is a nice way to implement the Merge type. The idea is to have a leader of each set. For example, if numbers 3, 5 and 8 are in the same set, then they might decide that 5 is their leader. You write a function leader(k) that returns the leader of the set that contains k. Then, to find out whether two numbers are in the same set, just check whether they have the same leader.
To implement the leader function, keep an array of integers called boss. If L is a leader, then boss[L] = L. That is, every leader is its own boss.
If number k is not a leader, then ideally boss[k] is the leader of the set containing k. Sometimes, however, the boss of a number is not its leader. But the leader of k is the same as the leader of the boss of k. By going to boss[k], at least you get closer to the leader. To find the leader of k, it suffices to perform the following loop.
r = k; while(boss[r] != r) r = boss[r];Now r is the leader of k.
When you are told to merge(m,n) what you need to do is
Find the leader r of m and the leader s of n.
Force r to be the boss (and leader) of s, by making boss[s] = r.
Now s is no longer its own boss. All numbers that have s as their boss now automatically have r as their leader, since the loop will not stop at s any more. It is very important that you only change the boss of a number that is currently its own boss, or the method will not work.
There are two ways to improve the efficiency of your implementation of the merge type. One involves a change to the leader function, the other a change to the merge function and to the representation of the abstract data type.
IMPORTANT. These improvements are part of the assignment, and you will lose points for not doing them. But only make these improvements after everything is working correctly without them. You will receive no credit for implementing these improvements if your basic implementation of the merge type does not work.
The first change involves a change to the leader function. After the leader function scans through a chain of boss links to find the leader of a number, it goes back through the chain and puts the genuine leader in the boss array, for every number that was looked at in the chain. That way, subsequent leader computations will go much more quickly. For example, if the boss array contains
boss[1] = 2 boss[2] = 4 boss[3] = 3 boss[4] = 6 boss[5] = 3 boss[6] = 6 boss[7] = 4 boss[8] = 5then computing leader(1) requires chaining through 1, 2, 4, 6, stopping at leader 6. The improvement adds another loop that changes the contents of the boss array to the following, by installing the correct leader (6) of each of the numbers that was looked at.
boss[1] = 6 boss[2] = 6 boss[3] = 3 boss[4] = 6 boss[5] = 3 boss[6] = 6 boss[7] = 4 boss[8] = 5It is just a matter of rescanning through the chain, the same way the chain was scanned the first time, but now putting the leader into the array as you go.
Notice that we have not scanned the entire boss array from beginning to end! Boss[8] is still 5, even though the leader of 8 is 3. Only the numbers that were looked at in the original scan have their boss values changed. If you try to change everything in the array, you make the implementation slower, not faster.
Also notice that it was not just the boss of 1 that was changed. All of the numbers that were examined in the chain have their bosss set to their leaders. For example boss[2] was changed too.
Each number that is a leader has a collection of constituents who have it as their leader. For example, in the above array, number 3 is a leader, and the constituents of 3 are 3, 5 and 8. So number 3 has three constituents, counting itself. The constituent count of a leader tells how many numbers are in the set that contains that leader.
When doing a merge, you find two values s and t that are leaders. You can then either change the boss of s to t (so s is no longer a leader) or change the boss of t to s (so t is no longer a leader). The choice of which to do influences the efficiency of the implementation. The best choice is to change the boss of the number that has the fewest constituents. That tends to keep the lengths of the boss chains up to the leader short.
Modify the data structure so that each number has not only a boss, but also a count of its constituents. A number that is not a leader has no constituents. So now the information is an array of structures, where each structure contains a boss and a constituent count.
A picture of the initial array, before any merges have been done, might look like this. Notice that each number has one constituent, itself.
index boss numConstituents
1 1 1
2 2 1
3 3 1
4 4 1
5 5 1
When doing a merge, compare the constituent counts. Change the boss of the value with the fewer constituents. (If they have the same number of constituents, then the choice is arbitrary. For example, change the first one.) If you change things so that the boss of s becomes t, then remember that all of the constituents of s become new constituents of t. For example, if you do merge(3,5) in the above array, you might arbitrarily decide to make the boss of 3 be 5. Then the array looks like this.
index boss numConstituents
1 1 1
2 2 1
3 5 0
4 4 1
5 5 2
If you now do merge(5,1), you must change the boss of 1,
since it has fewer constituents than 5. The array ends up looking like
this.
index boss numConstituents
1 5 0
2 2 1
3 5 0
4 4 1
5 5 3
As before, only change the boss of a number that
is currently a leader. If you now do merge(2,1), you
must realize that you are really being asked to merge 2 and 5, since
5 is the leader of 1. Since 5 has more constituents, you change
2, yielding
index boss numConstituents
1 5 0
2 5 0
3 5 0
4 4 1
5 5 4
As you can see, this improvement tends to lead to shorter chains
of bosses before the leader is found.
It is not guaranteed to ensure that the boss is
always the leader, though. You still need to do the
leader calculation using a loop.
Implement the Merge type as a class. Provide not only the merge and together operations, but also a constructor that takes a parameter n and builds a boss array for numbers 1,...,n. (Be careful. You might want to have n+1 spots in the array, since you will not use index 0.) The constructor should set boss[k] = k for each k from 1 to n, so that every number is a leader. That puts each number in a separate set initially. You can assume that n will be less than or equal to 100, but it must be very easy to change that assumption.
Keep as much private in the class as possible. There should be no public variables. Do not make a function public unless you need to, because it is one of the operations provided by the abstract data type. The leader function, for example, should be private.
Use the implementation method discussed here. Do not invent your own. In particular, be sure that neither the merge nor the together function performs a scan of every member of the boss array. That is not called for here, and it is much less efficient than what is described here.
You will need to produce a tester in order to check whether your implementation is working. Write a main program that creates some Merge objects, and performs some merge and together operations on them. Check the results. For debugging purposes, you can provide another public operation in the class that prints out the leader of each value. That way, you can check that things are working correctly.
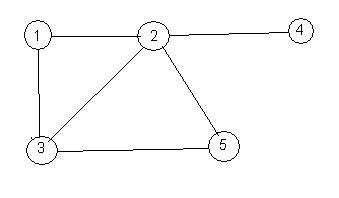
A graph is a collection of vertices connected by a collection of edges. An edge connects exactly two vertices to one another. You can draw a picture of a graph by showing the vertices and the edges connecting them. Here is an example. The vertices are shown as circles with numbers in them and the edges are lines connecting the vertices.

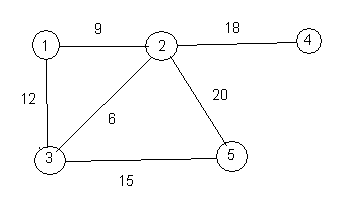
A weighted graph is a graph in which each edge has a number attached to it, called the weight of the edge. Here is a picture of a weighted graph.
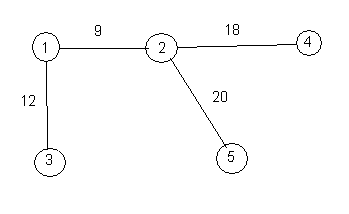
A spanning tree of a graph is obtained by deleting as many edges as possible, without making it impossible to get from any vertex to any other by following a sequence of edges. For example, the following is a spanning tree of the above weighted graph.
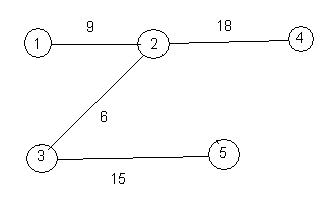
The weight of a spanning tree is the sum of the weights of its edges. For example, the weight of the above spanning tree is 59. Here is another spanning tree for the same graph. Its weight is 48.
Obviously, some spanning trees have smaller weight than others. A minimal spanning tree is a spanning tree with the smallest possible weight.
Suppose that we have a collection of towns, and we must build railroad tracks so that it is possible for a train to get from any town to any other town. Our budget for building tracks is small, so we choose to build as little track as possible. One approach to deciding which tracks to build is to construct a weighted graph, where the vertices are the towns, and the weight of the edge from town A to town B is the length of the railroad track that would need to be built to connect towns A and B directly. Then a minimal spanning tree of that graph would be a good choice for connecting the towns, since it is the cheapest way to connect all of the towns using railroad tracks between towns.
A similar problem occurs when a house is being wired for electricity. All of the outlets on a given circuit need to be connected to the circuit panel, and to each other. To connect them with a minimum amount of wire, you might build a graph having a vertex for each outlet and for the circuit panel, with the weight between two vertices being the wiring distance between those vertices. Then get a minimal spanning tree for the graph.
(A minimal spanning tree is not always the best solution to either of these problems. You can often do better by introducing new railroad track junctions or wiring junctions, called Steiner points. For example, if you have three towns in a triangle, you can connect them together by sending tracks to a point in the middle of the triangle. The middle point is a Steiner point. But good placements of Steiner points are difficult to find, so a minimal spanning tree is a reasonable compromise.)
Write a program that reads a description of a weighted graph, and prints the edges that are part of a minimal spanning tree of that graph, and also prints the total weight of the minimal spanning tree.
The input starts with a line that tells how many vertices the graph has. If there are five vertices, then those vertices have numbers 1, 2, 3, 4 and 5. In general, if there are n vertices, then they are numbered 1...n.
Following the first line are the edges, one per line. Each edge line has three integers on it. Line
2 4 50indicates that there is an edge between vertices 2 and 4, and that its weight is 50. The end of the input is signaled by a line that contains just a 0. An input describing graph

might look like this.
5 1 2 9 1 3 12 2 4 18 2 3 6 2 5 20 3 5 15 0The output of your program for this input might look like this.
The input graph has 5 vertices, and its edges are as follows. vertices weight 1 2 9 1 3 12 2 4 18 2 3 6 2 5 20 3 5 15 A minimal spanning tree uses the following edges. vertices weight 2 3 6 1 2 9 3 5 15 2 4 18 The total weight of the spanning tree is 48.
Your program is not required to insist that the three numbers that describe an edge are on one line, but it can if it wants to. For example, if your program allows an input like the following, that is acceptable. But your program is not required to allow such inputs. (You will find it easier to allow these additional input forms.)
5 1 2 9 1 3 12 2 4 18 2 3 6 2 5 20 3 5 15 0The only difference between this and the previous input is the placement of line breaks.
When designing a program, you need to decide how to represent your data. Typically, you draw diagrams showing arrays, structures, pointers, etc. to understand the data representation.
Once you have decided on a representation, you need to decide whether you want the data structure to be open or closed in your program.
Choosing an open data structure allows all parts of the program that use the data structure to see the exact representation, and to manipulate that representation directly. This has the advantage that you do not need to introduce any special functions to manipulate the data structure, and you have a lot of flexibility in how to use it. This approach has the disadvantage of making the form of data structure difficult to change. The code is also typically less readable than if you use a closed approach. Also, you often end up writing the same code to manipulate the data in more than one place in your program.
When you choose a closed representation, you are creating an abstract data type. Choosing a closed data structure involves hiding the representation inside a class or module, and only allowing the data to be accessed through public functions of the class or module. This typically involves more initial work, but makes your program easier to modify and often makes it easier to write in the long run.
For this program I will have mercy on you and allow you to use an open representation for graphs. You will find this a little simpler. If you prefer to use a closed representation (a class) that is fine. But only do that if you have a solid understanding of what you are doing.
Create a structure type Graph. You can store a graph as an array of edges, where each member of the array is a triple giving two vertex numbers and a weight. A triple is just a structure with three variables in it. Of course, you must also store the number of edges and the number of vertices, in addition to the array. Store those numbers once for the graph, not once for each edge. So the graph itself will be a structure holding the number of vertices, the number of edges and an array of edges.
You may presume that there will be a maximum of 100 edges in the graph, but you must design your program so that it is very easy to change the maximum number of edges to some other number.
Use sensible names for things. If something is an edge, don't call it a graph. Call it an edge. Do not call a vertex and edge, or a graph a vertex. Call things what they are.
Here is a simple algorithm for computing a minimal spanning tree of a weighted graph.
Create a new Merge object. The items in the sets are the vertices of the graph. Two items are in the same set if they are connected, using the edges that are currently in the tree. Since the tree initially has no edges, no two vertices are in the same set.
Create an array that will end up holding the edges of the spanning tree. Initially, it has no edges in it, but you gradually add more edges. Also create a count, initially 0, of the total weight of the edges in the spanning tree array. You will find it convenient to make the spanning tree description have type Graph. The spanning tree is a graph, after all.
If the array of edges of the graph is called G.edges, then sort the edges in G.edges by their weights, with smaller weights earlier in the array. (You can use function qsort, described below, to do this.)
Scan through the array G.edges in increasing order of weight. (That is, do the following in a loop.) When you see edge (i,j), with weight w, ask the Merge object whether vertices i and j are already connected. (They are connected if they are together.) If they are connected, then just skip this edge, and go to the next edge. If they are not connected then add edge (i,j) to the spanning tree, add w to the total weight of the tree, and tell the Merge object to merge i and j. Then do the next edge.
When you are finished, you will have created an array holding the edges of a minimal spanning tree of the original graph, and you will have computed the total weight. Print them all.
There is a standard library function called qsort that implements a variant of the quicksort algorithm for sorting arrays. You should include header file <cstdlib> to use qsort. This function is designed to be able to sort any kind of array into any desired order. In order to achieve this degree of generality, qsort needs information about the array and how to sort it.
The prototype for qsort is as follows.
void qsort(void *base,
size_t nel,
size_t width,
int (*compar) (const void *, const void *));
Parameter base is a "pointer" to the array that you want to sort.
Notice that its type is void*. That just means that qsort knows that
it is a pointer, but does not know what type of thing it points to.
Parameter nel is the number of elements in the array, and parameter width is the number of bytes occupied by each element. (Type size_t is typically the same as int, and is used for values that describe the size of an array.)
Parameter compar is a function. It is responsible for telling qsort the order in which you want the array sorted. qsort will sort into ascending order, according to what function compar says is ascending order. Function compar takes two parameters, which will be pointers to particular members of the array. compar(A,B) should return
| a negative number | if A < B | |
| 0 | if A = B | |
| a positive number | if A > B |
Here is what you can do to use qsort to sort an array of edges,
assuming each member of the array has type Edge, and Edge is defined
as follows.
struct Edge
{
int v1,v2,weight;
};
First, define a comparison function.
int compareEdges(const Edges* A, const Edge* B)
{
return A->weight - B->weight;
}
Define a new type, QSORT_COMPARE_TYPE, as follows.
typedef int (*QSORT_COMPARE_TYPE)(const void*, const void*);
To sort an array Arr of n edges, you use statement
qsort((void*) Arr, n, sizeof(Edge), (QSORT_COMPARE_TYPE)compareEdges);
We have passed qsort the array to sort, the number of elements, the number
of bytes occupied by each element (given by sizeof(long), since each
element has type long) and the
comparison function, cast to the appropriate type.
Here is a suggestion for how to implement this program. This is a refinement plan. It tells how to produce more and more of the program, gradually refining it until eventually it does the whole job. It is critical that a refinement plan have tests along the way, so that the part written so far is known to work. That way, if you get an error, it is almost always in the part of the program that was most recently written, and finding bugs is relatively easy.
Implement the Merge ADT. Test it. Do not do the improvements yet. Testing involves writing a test program that is not part of the finished product of the program. The extra work to write the tester is well worth it. Proceeding beyond this step with a faulty ADT will cause huge problems later. Your tester can create a Merge object and make a few connections. Then it can ask if a few vertices are connected. Ask some questions where the answer should be yes, and some where the answer should be no. Check that the answers are correct.
Implement the part of the program that reads in and prints out the input graph. Test it. It is a good idea to use functions. You will need to print other graphs later.
Implement the beginnings of the minimal spanning tree algorithm by sorting the edges and printing them after sorting. Be sure that this is working.
Implement the rest of the minimal spanning tree algorithm. Test it. Look at the results. Are they correct? You will have to solve an example by hand to make sure.
Make the program's output look nice, if necessary. Test it.
Implement the improvements to the Merge data type. Test your program again. Notice how nice it would be to have an automated tester, so that you can easily retest your program when the improved Merge implementation is installed.
When you do a test, if things don't work, then use the debugger or add some prints to see what is going on. Do not try to work in the dark. Before you try to fix the problem, understand what is wrong. After you have diagnosed the problem, fix it. Do not move on until everything that you have written so far is working.
Place the Merge ADT in files called merge.h and merge.cpp. Make file merge.h contain the class, and merge.cpp contain the implementation details.
Call the class Merge, not something else. Call the methods merge and together.
Call the program that performs the minimal spanning tree computations mst.cpp.
Your program should read the graph description from the standard input, and write the results to the standard output.
Turn in all of your source files. Be sure that your name is in every source file. Turn in a Makefile for the program. Use the submit program. Version 1 is assignment 2a, and version 2 is assignment 2b. So to turn in version 1, you would use command
~karl/3510/bin/submit 2a merge.h merge.cpp mst.cpp Makefile
If you have questions, be sure to ask, and do so as soon as possible, so that you have time to deal with the response.