CSCI 3300
Fall 2013
Exercises for Quiz 7

1. Which of the following is true about log₂(500)?

   1. 6 < log₂(500) < 7
   2. 8 < log₂(500) < 9
   3. 10 < log₂(500) < 11
   4. 250 < log₂(500) < 251
   5. 499 < log₂(500) < 501

   Answer

2. How much time does Heapsort take to sort an array of n integers in the worst case?

   1. O(log₂(n))
   2. O(n)
   3. O(n log₂(n))
   4. O(n/log₂(n))
   5. O(n²)

   Answer

3. To within a constant factor, how much time does it take to insert a value into a height-balanced binary search tree that has n values in it already, in the worst case?

   Answer

4. To within a constant factor, how much time does it take to remove a value from a height-balanced binary search tree that has n values in it already, in the worst case?

   Answer

5. What is log₂(32)?

   Answer

6. Does the height-balancing algorithm based on single and double rotations always keep a tree height-balanced, or are there some rare sequences of insertions and removals that can cause the tree to become non-height-balanced?

   Answer

7. To within a constant factor, how much time does it take, on average, to look up a value into a hash table that has n values in it?

   Answer

8. To within a constant factor, how much time does it take, on average, to insert a value into a hash table that has n values in it?

   Answer

9. Would a hash table be a useful tool for sorting an array? Why or why not?

   Answer

10. Suppose that a linked list is used to store a set of numbers. If there are n numbers in the list, how long, to within a constant factor, does it take to check whether a given number is in the list, in the worst case?

    Answer

11. If you insert 6 into the following min-heap, then reorder to restore the heap order, what heap do you get?

    

    Answer

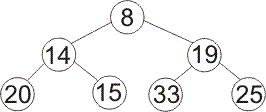
12. If you remove the smallest value from the following min-heap, then reorder to restore the heap order, what heap do you get?

    

    Answer

13. If you insert 10 into the following min-heap, then reorder to restore the heap order, what heap do you get?

    

    Answer

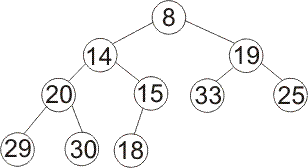
14. If you remove the smallest value from the following min-heap, then reorder to restore the heap order, what heap do you get?

    

    Answer

15. Type Node is shown at the bottom of the page. It is used as the node type for binary search trees.

    Assume that function insert(x,t) is available to you, where insert(x,t) inserts x into binary search tree t, modifying t.

    Write a definition of function insertAll(s,t), which takes two binary search trees s and t and inserts all members of tree s into tree t.

    Answer

struct Node
{
  int item;
  Node* left;
  Node* right;
  Node(int i, Node* L, Node* R)
  {
    item = i;
    left = L;
    right = R;
  }
};