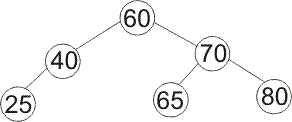
If you insert 26 into the following binary search tree using the algorithm that keeps the tree height-balanced by doing rotations, what tree do you get?
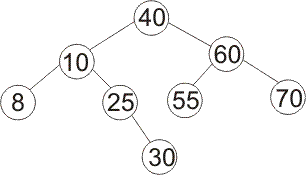
If you insert 27 into the following binary search tree using the algorithm that keeps the tree height-balanced by doing rotations, what tree do you get?
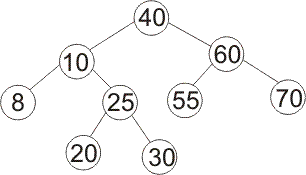
If you insert 20 into the following binary search tree using the algorithm that keeps the tree height-balanced by doing rotations, what tree do you get?

If you insert 27 into the following binary search tree using the algorithm that keeps the tree height-balanced by doing rotations, what tree do you get?
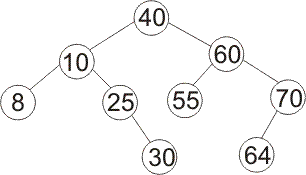
If you remove 8 from the following binary search tree using the algorithm that keeps the tree height-balanced by doing rotations, what tree do you get?

If you remove 40 from the following binary search tree using the algorithm discussed in class, without rebalancing, what binary search tree do you get?

If you remove 40 from the following binary search tree using the algorithm that keeps the tree height-balanced by doing rotations, what tree do you get?
What is log2(32)?
To within a constant factor, how much time does it take to insert a value into a height-balanced binary search tree that has n values in it already, in the worst case?
To within a constant factor, how much time does it take to remove a value from a height-balanced binary search tree that has n values in it, in the worst case?
Does the height-balancing algorithm based on single and double rotations always keep a tree height-balanced, or are there some rare sequences of insertions and removals that can cause the tree to become non-height-balanced?
The following questions use the following type Node.
struct Node
{
int item;
Node* left;
Node* right;
node(int i, Node* L, Node* R)
{
item = i;
left = L;
right = R;
}
};
The height of a tree is the number of nodes on the longest path from the tree's root to a leaf. An empty tree is defined to have height 0.
A tree is full if (1) all of its leaves have the same height, and (2) all nonleaves have two nonempty subtrees. By definition, an empty tree is full.
Write a function that takes a tree t, given by a pointer to its root, and returns the height of tree t if t is full, but returns -1 if tree t is not full.
Assume that function insert(x,t) is available to you, where insert(x,t) inserts x into binary search tree t, modifying t.
Write a definition of function insertAll(s,t), which takes two binary search trees s and t and inserts all members of tree s into tree t.
The following question uses the following type Cell.
struct Cell
{
Cell* next;
int item;
Cell(int i, Cell* n)
{
item = i;
next = n;
}
};
Write a function stutter(L) that takes a list L, of type Cell*, and yields a new list consisting of two copies in a row of each member of list L. For example, stutter([2,4,6,8]) = [2,2,4,4,6,6,8,8]